1-tan^2x identity 272450-Prove the identity 1+tan^2x/2tanx=csc2x

 Is tan^2x1=secx a pythagorean identityThe Pythagorean identity tells us that no matter what the value of θ is, sin²θcos²θ is equal to 1 We can prove this identity using the Pythagorean theorem in the unit circle with x²y²=1 Created by Sal Khan Google Classroom Facebook TwitterFree multiple angle identities list multiple angleLearn how to solve trigonometric identities problems step by step online Prove the trigonometric identity 1tan(x)^2=sec(x)^2 Applying the trigonometric identity \tan(x)^21=\sec(x)^2 Since both sides of the equality are equal, we have proven the identity Get an answer for 'verify (1 tan^2x)/(tan^2x) = csc^2x' and find homework help for other Math questions at eNotes Verify the identity `1/(tan^2x) 1/(cot^2x) = csc^2x sec^2x` 2

Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube

Prove the identity 1+tan^2x/2tanx=csc2x

Prove the identity 1+tan^2x/2tanx=csc2x-2 x I started this by making sec 1/cos and using the double angle identity for that and it didn't work at all in any way ever Not sure why I can't do that, but something was wrong Anyways I looked at the solutions manual and they magic out 1 tan ⁡ x tan ⁡ 2 x = 1 tanI just want to ask The equation says tan2x=2tanx/1tan^2x How did it become 2tanx and 1tan^2x?

2

 Simplify the expression using trig identities 1 (sin4x cos4x)/(sin2x cos2x) 2 (sinx(cotx)cosx)/(2cotx) Math Prove the identity sec^4x tan^4x = 12tan^2x Trig Use the fundamental identities to simplify the expression cot beta sec beta I used 1tan^2u=secu since cot is the inverse of tanB) (tanx 1) (tanx1)/1 tan^2 (x) =Math\sin^2x\cos^2x=1/math math\implies\dfrac{\sin^2x}{\cos^2x}\dfrac{\cos^2x}{\cos^2x}=\dfrac{1}{\cos^2x}/math math\implies\left(\dfrac{\sin x}{\cos x

A follow up proof to accompany sin^2 cos^2 =1 Another identity that is used quite a bit, especially in calculus involving trigonometric functionsTanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx tanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx Integral of the function \frac {\cos ^2 x} {1\tan x}Sec2 (x)(1 − sin2 (x)) = 1 sec 2 ( x) ( 1 sin 2 ( x)) = 1 Start on the left side sec2(x)(1−sin2(x)) sec 2 ( x) ( 1 sin 2 ( x)) Apply pythagorean identity sec2(x)cos2(x) sec 2 ( x) cos 2 ( x) Convert to sines and cosines Tap for more steps Apply the reciprocal identity to sec ( x) sec ( x)

Answers Click here to see ALL problems on Trigonometrybasics Question I need to prove the identity (1tan^2x)cot^2x=csc^2x Found 2 solutions by Alan3354, Regrnoth Answer by Alan3354 () ( Show Source ) You can put this solution on YOUR website!Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify Statistics Arithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution 1tan^2(x) = 1 (sin2x)/(cos2x) = cos2x sin2x/cos2x = cos 2x/cos2x is a posibly 'simplified' version in that it has been boiled down to only cosines

Www Birmingham K12 Mi Us Cms Lib Mi Centricity Domain 976 Chapter 5 Pdf

Tan 2x Tan 2x

I know that and The next step would then be to say that but now what?1 sin 2x = 1 sin 2x (Pythagorean identity) Therefore, 1 sin 2x = 1 sin 2x, is verifiable HalfAngle Identities The alternative form of doubleangle identities are the halfangle identities Sine • To achieve the identity for sine, we start by using a doubleangle identityThese identities are useful whenever expressions involving trigonometric functions need to be simplified An important application is the integration of nontrigonometric functions a common technique involves first using the substitution rule with a trigonometric function, and then simplifying the resulting integral with a trigonometric identity

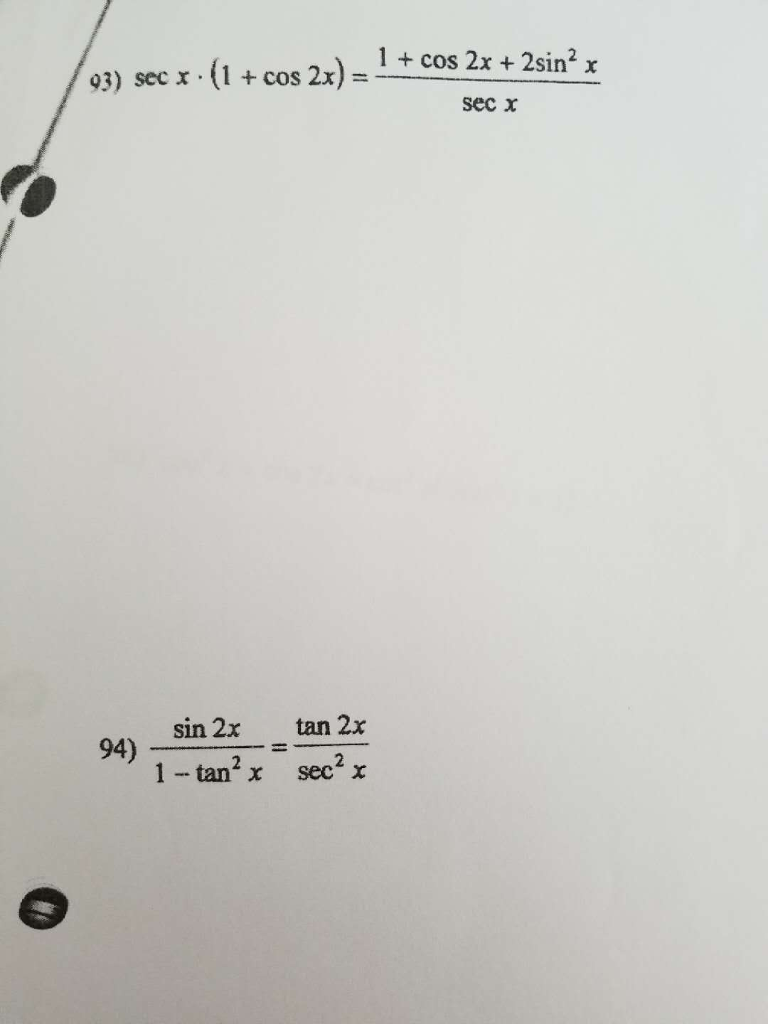
Solved Verify Each Identity Solve As A Two Column Proof Chegg Com

Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x

The trigonometric identity `(tan^2x)/(1tan^2x) = sin^2x` has to be proved Start with the left hand side `(tan^2x)/(1tan^2x)` Substitute `tanx = sin x/cos x`Learn how to solve trigonometric identities problems step by step online Prove the trigonometric identity 1tan(x)^2=sec(x)^2 Applying the trigonometric identity \tan(x)^21=\sec(x)^2 Since both sides of the equality are equal, we have proven the identityVerify this identity (tan^2 (x)1)/ (1tan^2 (x)) = 12cos^2 (x) I've started a couple different options but none are working out for me Here is what I have so far A) multiply top by (1 tan^2 (x)) to get tan^4 (x) 1 or (tan^2 (x)1) (tan^2x1) then i'm stuck!

1

How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic

 Prove the identity 1tan^2x/2tanx=csc2x1 1 Because the two sides have been shown to be equivalent, the equation is an identity cos2(x)(1tan2(x)) = 1 cos 2 (x) (1 tan 2 (x)) = 1 is an identity1 cos ( x) − cos ( x) 1 sin ( x) = tan ( x) Go!Verifying the identities illustrates how expressions can be rewritten to simplify a problem Simplifying one side of the equation to equal the other side is a method for verifying an identity See Example \(\PageIndex{1}\) and Example \(\PageIndex{2}\) The approach to verifying an identity depends on the nature of the identityTrigonometric identities Intro to Pythagorean trigonometric identities Converting between trigonometric ratios example write all ratios in terms of sine Practice Evaluating expressions using basic trigonometric identities Trigonometric identity example proof involving sec, sin, and cos

Answered Trigonometric Identities And Equations Bartleby

Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf

Introduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formulaCorrect answers 3 question Verify the identity (1 tan^2x)(1 sin^2x) = 1 i know the solution, but not the steps to get me the answers i need i will need to know how to do this on my own for a test soon, so any explanations will be appreciated solution, kinda (1 tan^2x)(1 sin^2x) = sex^2x * cos^2x = 1/cos^2x = 1 here are some identities that i'm pretty sure need to be used, but i'mProve the identity 2tanx/1tan^2x=sin^2x 11,8 results, page 18 trig If sin theta is equal to 5/13 and theta is an angle in quadrant II find the value of cos theta, sec theta, tan theta, csc theta, cot theta Math Find the values of the six trigonometric functions of

How Do You Prove Cosx Cscx 2sinx Tanx 1 Tan 2x Socratic

Wl Apsva Us Wp Content Uploads Sites 38 15 05 Lesson 6 4 Notes 1 Pdf

 Explanation 1 − tan2x 1 tan2x = 1 − sin2x cos2x 1 sin2x cos2x = cos2x−sin2x cos2x cos2xsin2x cos2x = cos2x −sin2x cos2x sin2x = cos2x −sin2x =Because the two sides have been shown to be equivalent, the equation is an identity Trig identities how does tan2x=2tanx/1tan^2x become 2tanx and 1tan^2x?

Http Www Math Brown Edu Tomg Formulas Pdf

Answered Prove The Identity 1 Tanx Sec 2x 2 1 Bartleby

Mmm4444bot Super Moderator Staff member Sec^2x=1tan^2x proofD is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4Verify the identity {eq}\sec^4x \sec^2x = \tan^4x \tan^2x {/eq} Verifying a Trigonometric EquationIdentities related to sin 2x, cos2x, tan 2x, sin3x, cos3x, and tan3x Sin 2x = Sin 2x = sin(2x)=2sin(x) cos(x) Sin(2x) = 2 * sin(x)cos(x) Proof To express Sine, the formula of "Angle Addition" can be used

Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions

Which Of The Following Are Trigonometric Identitie Gauthmath

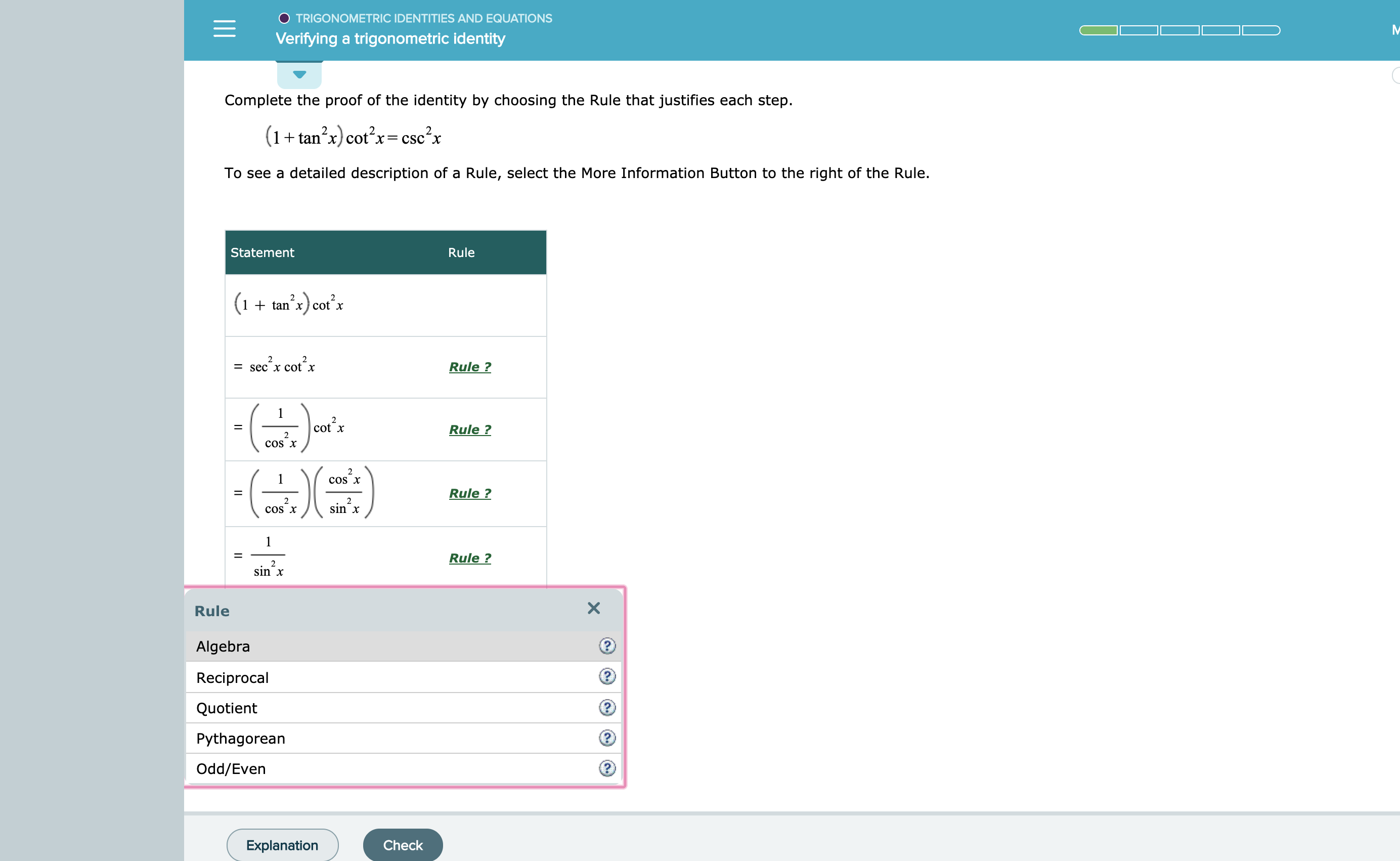
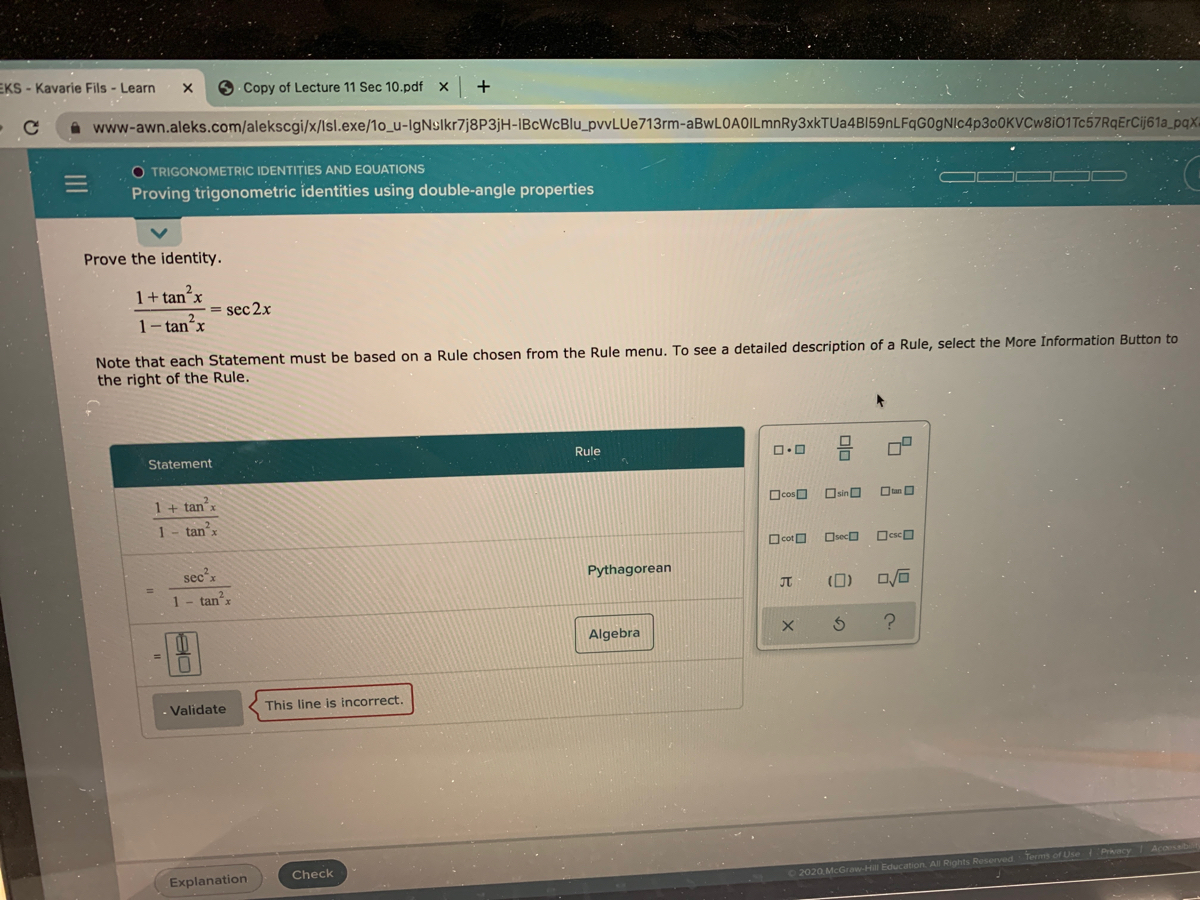
The Pythagorean Identities are based on the properties of a right triangle cos2θ sin2θ = 1 1 cot2θ = csc2θ 1 tan2θ = sec2θ The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle tan(− θ)Various identities and properties essential in trigonometry Legend x and y are independent variables, d is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x /cos x equation 1Tan^2x1 identity Tan^2x1 identityYou can put this solution on YOUR website!Verify the identity {eq}1 \tan^2x = \frac{\cos2x}{\cos^2x} {/eq} Identity An identity is an equation that holds true for any given variable value We have many commonly used trigonometric

Www Jensenmath Ca Unit 5 pretest review solutions Pdf

Http Www Pstcc Edu Facstaff Jwlamb 1730 7 3 Pdf

 Having some trouble proving this identity (CosX 1)/ (tan^2x) = (CosX)/ (secX 1) Click to expand IF you recognize (from the fundamental identities) that sec^2 x 1 = tan^2 x, then working with the righthand side should be obvious Multply numerator and denominator of the righthand side by (sec x 1) cos x (sec x 1)Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreVerifying Trigonometric Identities 2 cos 2⁡x − 1 = 1 − tan 2⁡x 1 tan 2⁡x Ask Question Asked 8 years, 4 months ago Active 8 years, 4 months ago Viewed 1k times

Http Www Wssd Org Cms Lib02 Pa Centricity Domain 140 1 4 1 6 Pdf

Verify The Given Identity Tan 2x 2 Cot X Tan X Chegg Com

Free math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantlyYou could take tan(x) out of the fraction, but I still don't know how to go about simplifying it The book says the answer isSin^2x tan^2x cos^2x = 1tan^2x use the identity tan^2x 1 = sec^2x thus sin^2x tan^2x cos^2x = 1tan^2x = sec^2x hence proved tan^2x(cos^2x1)Cos^2x=Sec^2x

Prove The Identity 1 Tan 2x 1 Tan 2x 1 2sin 2x In Urdu Hindi Youtube

Simplify Without Using A Calculator Frac Cos 210 Gauthmath

We know the identity sin 2 (x)cos 2 (x)=1 ——(i) Dividing throughout the equation by cos 2 (x) We get sin 2 (x)/cos 2 (x) cos 2 (x)/cos 2 (x) = 1/cos 2 (x) We know that sin 2 (x)/cos 2 (x)= 1tan^2x identity Is sec^2x1=tan^2x an identity Trigonometry Identity tan^2 (x) 1 = sec^2 (x) Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device Up next in 8Because the two sides have been shown to be equivalent, the equation is an identity (1−sin2 (x))(1tan2 (x)) = 1 Account Details Login Options Account Management Settings The power reducing identities allow you to write a trigonometric function that is squared in terms of smaller powers The proofs are left as examples and review problems \(\sin ^2x=\dfrac{1−\cos 2x}{2}\) \(\cos ^2x=\dfrac{1\cos 2x}{2}\) \(\tan ^2x=\dfrac{1−\cos 2x}{1\cos 2x}\) Power reducing identities are

How Do You Prove Tan 2x Secx 1 1 Secx Socratic

Trig Find Tan X Given Tan 2x 2 Pi X 3pi 2 Cheatatmathhomework

 prove the identity (tan^2x1)(cos^2x1)= tan^2x Recently Posted Assignment Question R A large arge Ponee is filled from a garden hose at the rate哗In mathematics, an "identity" is an equation which is always true These can be "trivially" true, like "x = x" or usefully true, such as the Pythagorean Theorem's "a 2 b 2 = c 2" for right triangles There are loads of trigonometric identities, but the following areK ken_165 New member Joined Messages 11 #1 Hello!

Reciprocal Identities In Trigonometry With Examples Owlcation

2

Www Kpu Ca Sites Default Files Faculty of science 26 horticulture Mathematics Algtrig Studsol Ch9 Pdf

Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube

Double Angle Trigonometric Identity Archives Sat Prep

Secx Cosx Cscx Sinx Tanx 1 Tan 2x Trigonometric Identity 2mvi 0934 Youtube

Sin2x Cos2x 1 Proof

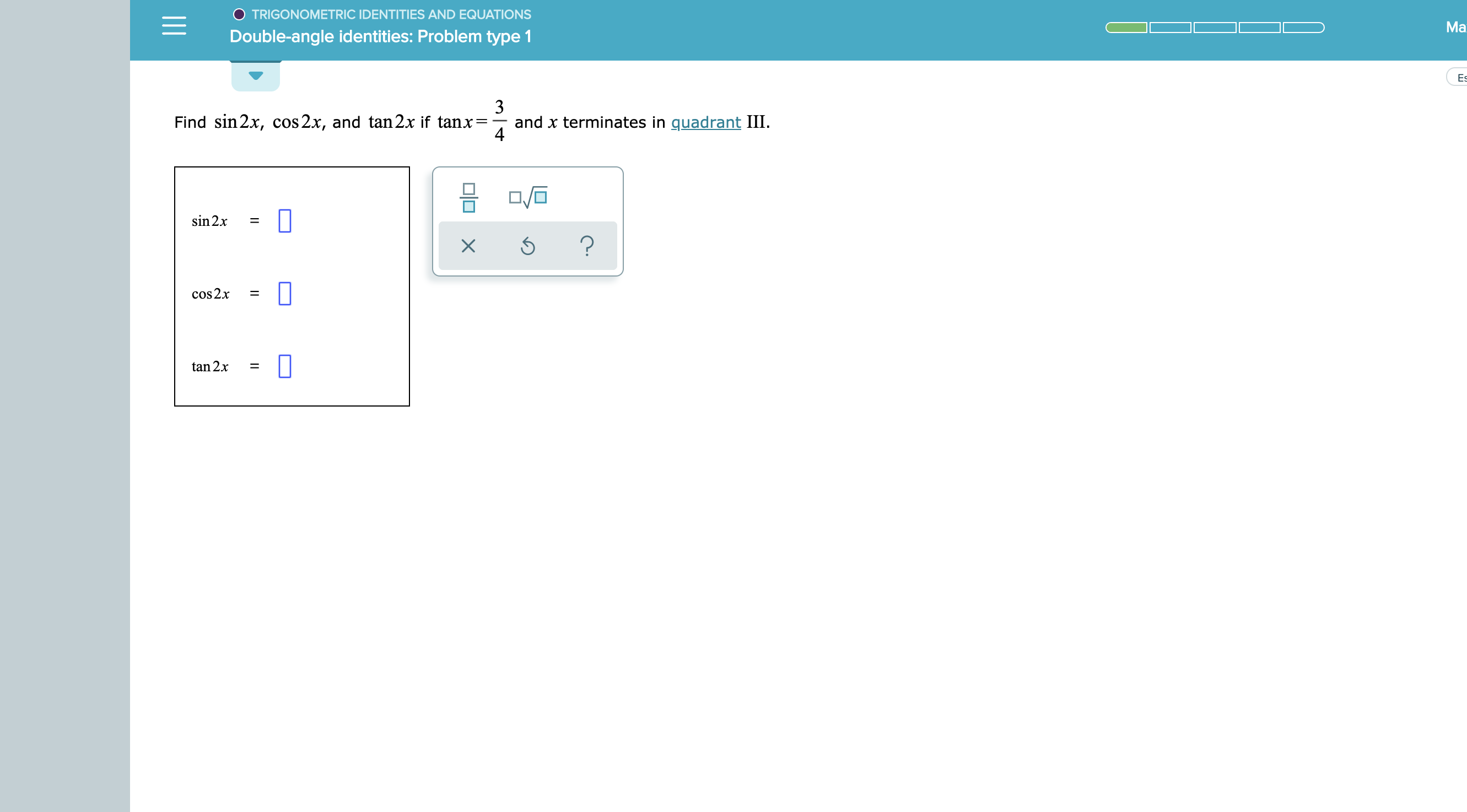
Solved Find Sin2x Cos2x And Tan 2x If Cosx And X Ter Chegg Com

2

1 8 Verify Each Identity 1 Tan Sin Cos Sec Chegg Com

How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic

Verify Identity Tan 2 X 1 Tan X Sec X 1 Sin X Cos 2 X Youtube

Half Angle Identities

Trigonometric Identity With Pythagorens Sec 2x Sin 2x Cos 2x Tan 2x Youtube

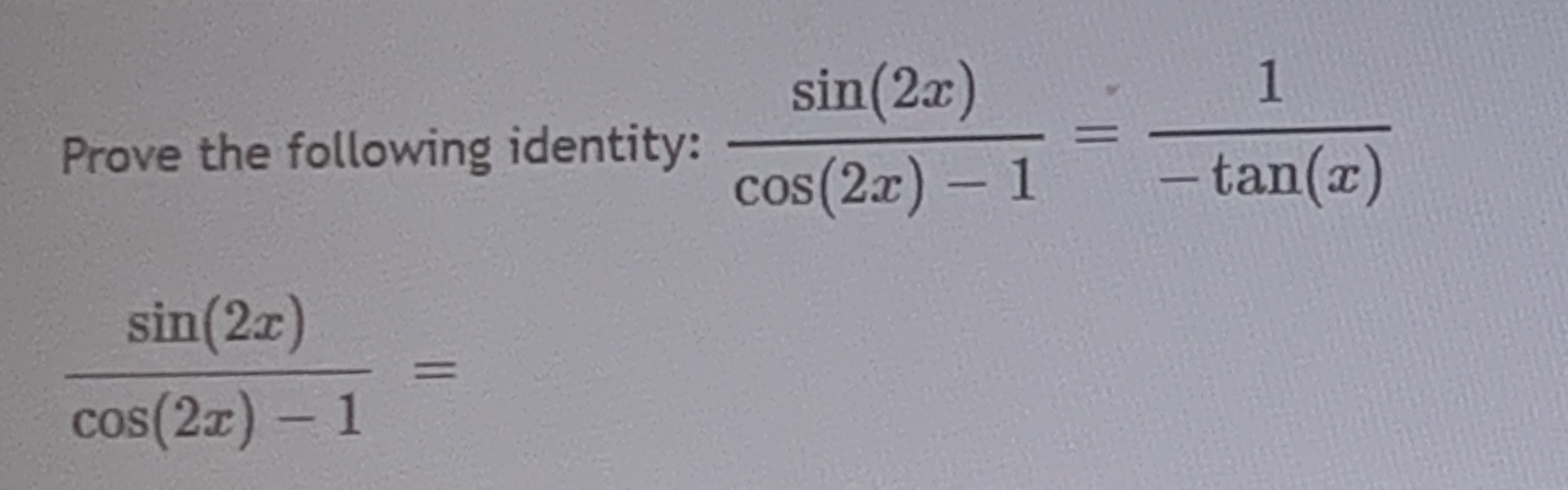
Answered Sin 2x 1 Prove The Following Identity Bartleby

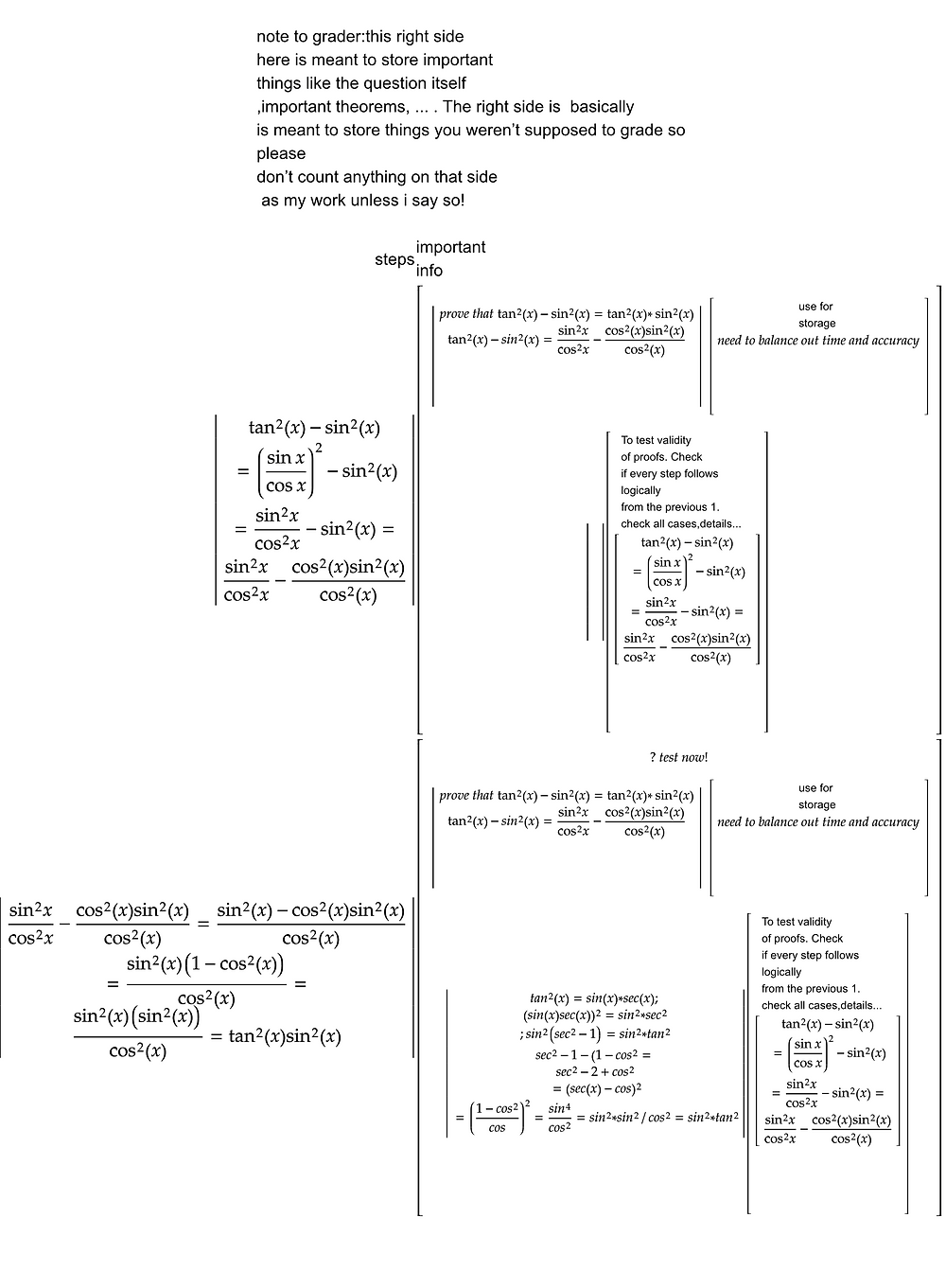
Can Someone Help Me Prove This Trigonometric Identity Tan 2x Sin 2x Tan 2x Sin 2x Blackpenredpen

If Sin X 1 5 And X Is In Quadrant I Find The Exact Values Of The Expressions Without Solving For X Wyzant Ask An Expert

Trigonometry Identities And Equations Ppt Download

Derive 1 Tan 2x Sec 2x And 1 Cot 2x Text Cosec 2x Geometrically Mathematics Stack Exchange

Trig Identity Sec 4x Tan 4x 1 2tan 2x Youtube

Ppt Analytic Trig Powerpoint Presentation Free Download Id

Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo

Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube

Cos Sin Tan Csc Sec Cot

3

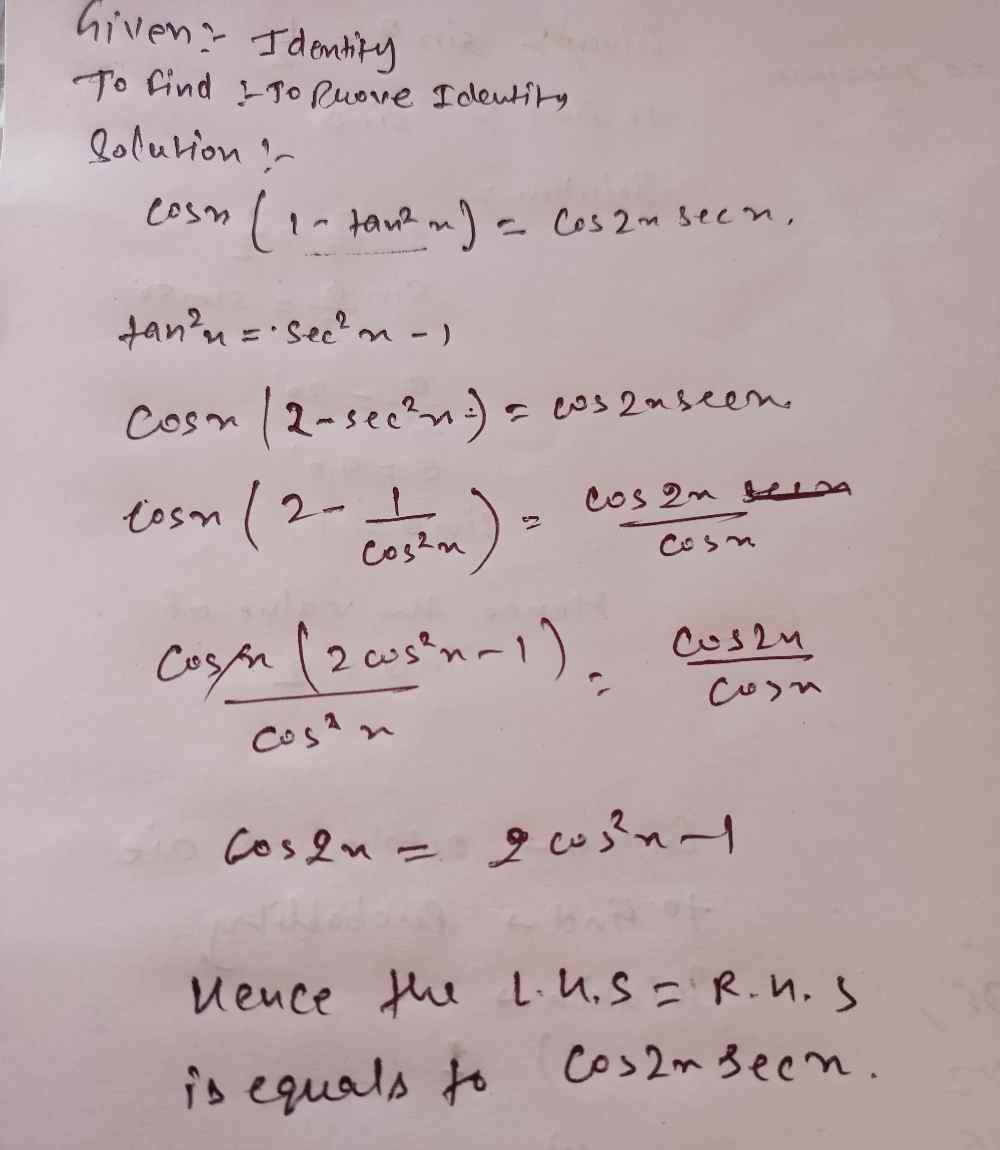
Prove The Following Identities 10 Cos X 1 Tan Gauthmath

Topic Lesson Trigonometric Functions

Example 27 Find Value Of Tan Pi 8 Chapter 3 Class 11

Every Day I M Calculatin I D3 Unit Q Pythagorean Identities

Basictrigonometry Pdf Trigonometric Functions Sine

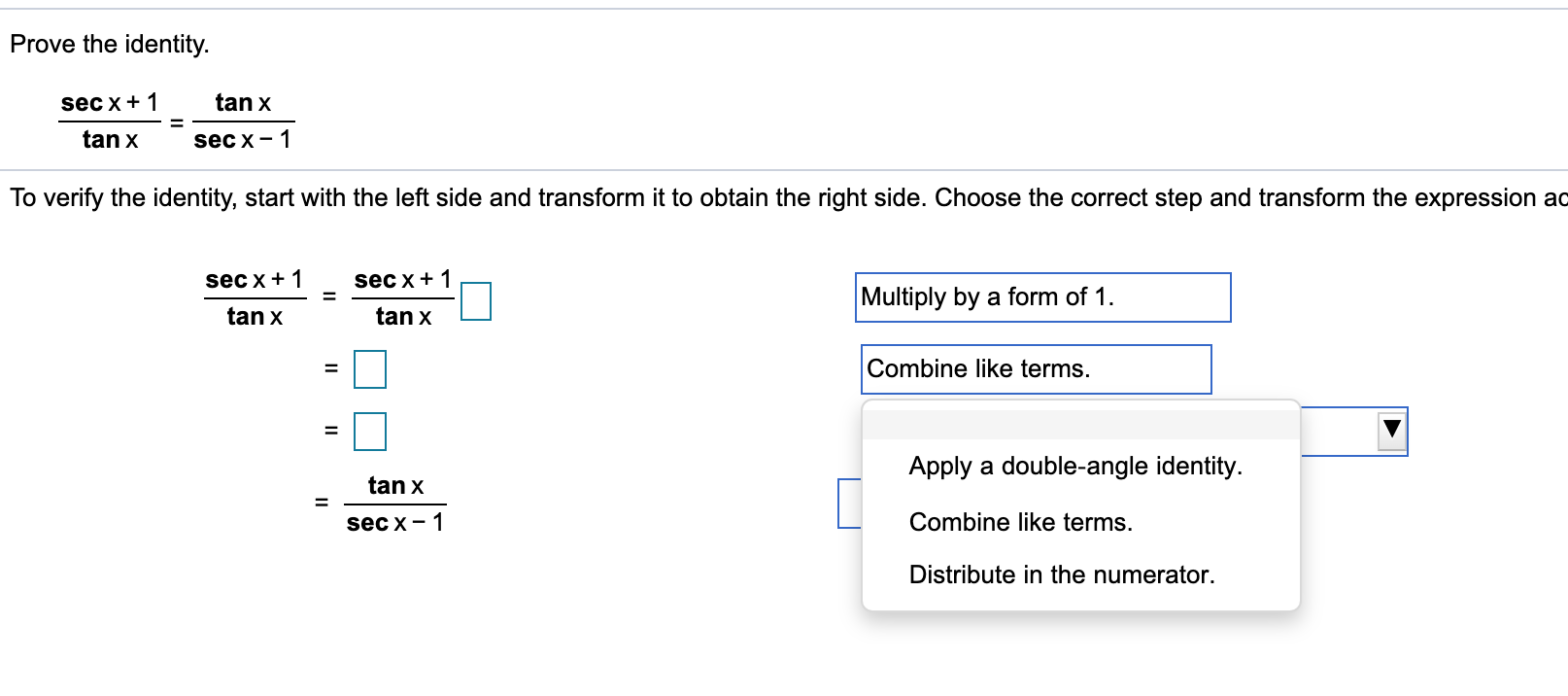
Prove The Identity Sec X 1 Tan X Tan X Secx 1 To Chegg Com

Packet 21 Trigonometric Identities Ppt Download

Tan 2x Csc 2x Tan 2x 1 Problem Solving Solving Identity

Http Www Pitt Edu Evt3 Triviums Trigonometry Trivium Pdf

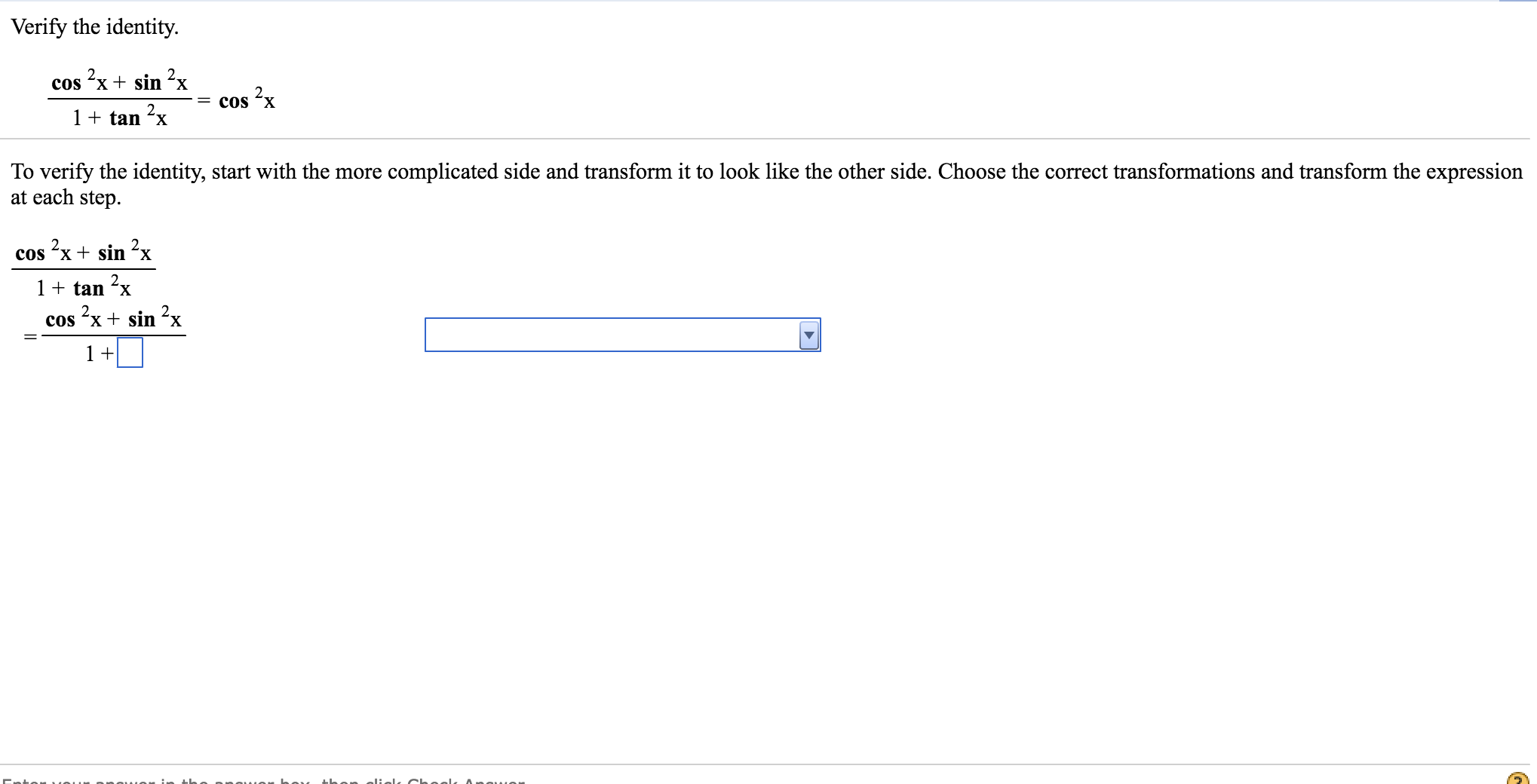
Verify The Identity Cos 2x Sin 2x 1 Tan 2x Chegg Com

2

Using Trigonometric Identities Video Khan Academy

Web Stanford Edu Class Archive Math Math Math 1144 Files Trig Pdf

Q Tbn And9gcr2jamezvnschsup9wyxdzj0wc0knie4dqfphj6okqiboct8vn1 Usqp Cau

Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube

Trigonometric Identity Examples Solutions Videos

Trigonometric Identities Trigonometric Functions Trigonometry

Solved Complete The Sentence So The Result Is An Identity Let X Be Any Real Number 1 Sin 2 X Cot 2 X Cos 2 X Sec 2 X Tan 2 X Complete The Sent Course Hero

Www Birmingham K12 Mi Us Cms Lib Mi Centricity Domain 976 Chapter 5 Pdf

Trig Identity Sec2x Minus Tan2x T10 Youtube

Rd Sharma Solutions For Class 11 Chapter 5 Trigonometric Functions

Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco

How Do You Prove Tan 2x Secx 1 1 Secx Socratic

Http Www Whsd K12 Pa Us Userfiles 1598 Classes 9713 Trig chapter 5 notes Pdf

Answered 3 1 Tanx Tan 2x Sec 2x S Bartleby

Solving Trigonometric Proofs Cheat Sheet By Lwaites Download Free From Cheatography Cheatography Com Cheat Sheets For Every Occasion

How Do You Prove That Tanx Secx 1 Tanx Secx 1 1 Sinx Cosx Socratic

Http Ww2 Justanswer Com Uploads Ryanp97 12 04 05 Solutions3 Pdf

Tan 2x Tan 2x

What Is The Derivative Of Tan 1 Sec X Tan X Quora

Slides Show

Answered O Trigonometric Identities And Bartleby

How Many Can You Derive From First Principles Ppt Download

Double Angle And Half Angle Identities Example Sin 28 Cos 2a Or Tan 2x

Www Rusdlearns Net C File Show

The Expression 1 Tan X Tan 2 X 1 Cot X Cot 2 X Has The Positive Values For X Given By

3

Double Angle Formulas What Are Double Angle Formulas Examples

Trigonometry Reciprocal Identities Expii

Wl Apsva Us Wp Content Uploads Sites 38 15 05 Lesson 6 4 Notes 1 Pdf

Ppt 5 1 Fundamental Trig Identities Powerpoint Presentation Free Download Id

Trig Identities Crossword Wordmint

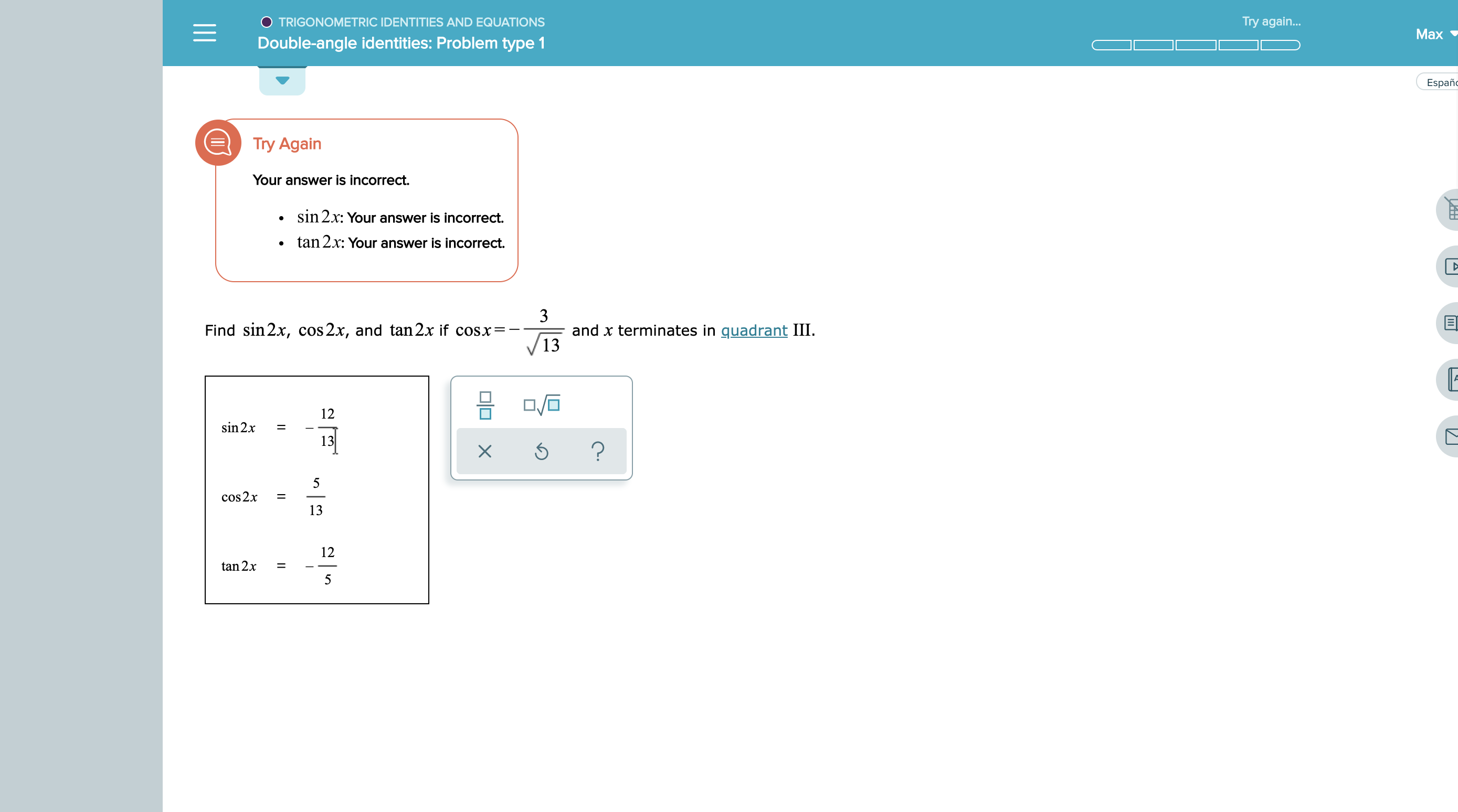
Answered Try Again Trigonometric Identities Bartleby

Http Scibug Com Public Docs Trigonometry Cheat Sheet Pdf

Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf

Http Theprofessorshut Weebly Com Uploads 2 3 2 7 Pc Chap 6 Sect 2 Sum Difference And Cofunction Identities Pdf

What Basic Trigonometric Identity Would You Use To Gauthmath

X Y X Y X Y X Y Ppt Download

How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Socratic

Tan2x ただの悪魔の画像

How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic

Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco

Reciprocal Identities In Trigonometry With Examples Owlcation

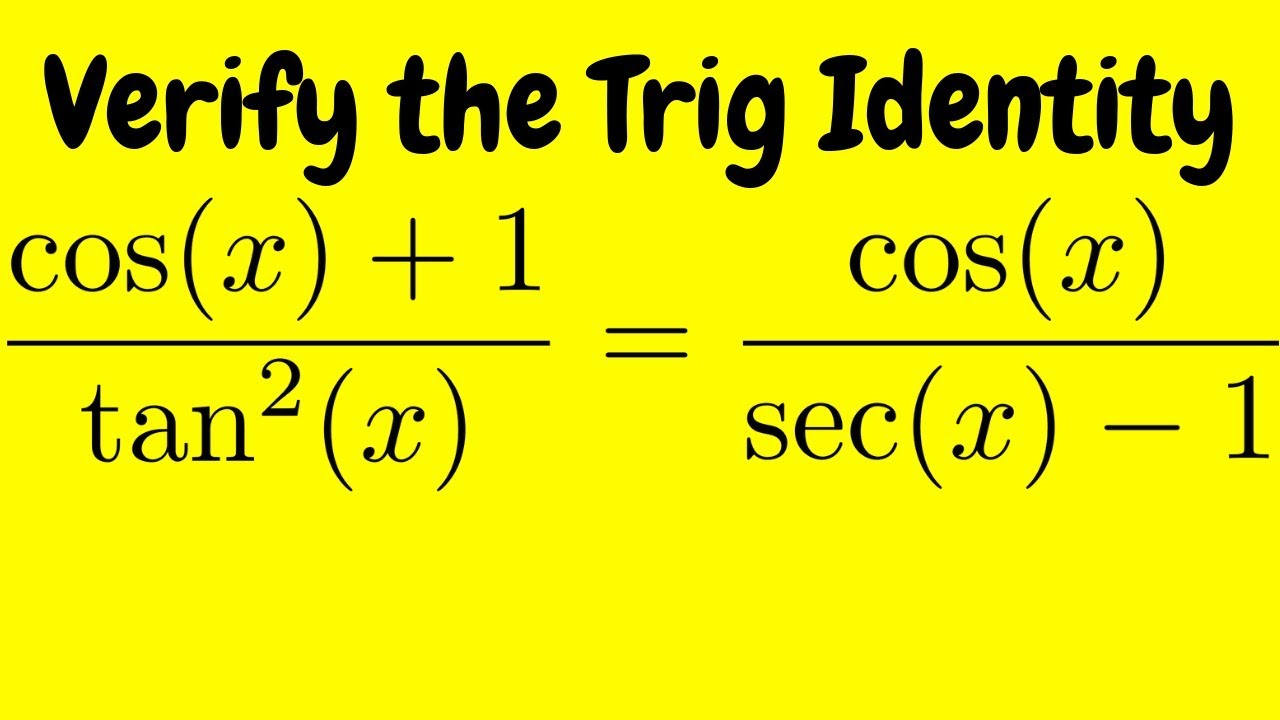
Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube

Prove Or Disprove The Identity If You Find The Identity Is True State The First Line Of The Proof Brainly Com

1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube

Tan 2x Formula What Is Tan 2x Formula Examples

Incoming Term: 1-tan^2x identity, prove the identity 1+tan^2x/2tanx=csc2x, is sec^2x-1=tan^2x an identity, what is 1-tan^2x,