If f(2tanx/1 tan^2x)=(1 cos2x)(sec^2x 2tanx)/2 then f(4)= 136355

 Transcript Ex 72, 25 1 2 1 tan 2 Step 1 Let 1 tan = Differentiating both sides 0 sec 2 = sec 2 = = sec 2 = 1 cos 2 = cos 2 Step 2 Integrating the function 1 2 1 tan 2Share with your friends Share 02 tan x = 2 ( sin x )/ ( cos x ) (1) = 2 ( sin x )( cos x )/ (cos²x ) = ( sin 2x ) (sec²x ) ( Since, 1/ cos²x = sec²x ) = ( sin 2x

Tan2x ただの悪魔の画像

If f(2tanx/1 tan^2x)=(1 cos2x)(sec^2x 2tanx)/2 then f(4)=

If f(2tanx/1 tan^2x)=(1 cos2x)(sec^2x 2tanx)/2 then f(4)=-Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more Transcript Example 28 If tan⁡𝑥 = 3/4 , "π" < 𝑥 < 3𝜋/4 , find the value of sin 𝑥/2 , cos 𝑥/2 and tan 𝑥/2 Given that "π" < x < 3𝜋/2 ie180° < x < 3/2 × 180° ie 180° < x < 270° Dividing by 2 all sides (180°)/2 < 𝑥/2 < (270°)/2 90° < 𝑥/2 < 135° So, 𝑥/2 lies in 2nd quadrant In 2nd quadrant, sin is

Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube

 Prove $$\frac{2\tan x}{1\tan^2x}\frac1{2\cos^2x1} = \frac{\cos x\sin x}{\cos x\sin x}$$ I know how to solve it, yet I can't!Verify that $$ 2\cos^2x1 = \frac{1\tan^2x}{1\tan^2x}$$ Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careersI need to use the fact that $\tan 2x=\sin2x \ /\cos2x$ to prove that $$\tan 2x=\frac{2\tan x}{1\tan^2x}$$ I don't know where to start Please help or hint Thanks in advance

Tan2x1 = sec2x sin 2x = 2 sin x cos x cos 2x = 2 cos2x 1 tan x = sin x cos x sec x = 1 cos x cot x = cos x sin x csc x = 1 sin x Some integration formulas R xn dx = xn1 n1 C R 1 x dx = lnjxjC R ex dx = ex C R sin x dx = cos x C R cos x dx = sin xC RB) (tanx 1)(tanx1)/1 tan^2(x) = (sinx/cosx 1)(sinx/cosx 1) / 1 Use trig identities 1 tan^2 x = 1/cos^2 x = sec^2 x (1 tan x) = 1 tan^2 x 2tan x = sec^2 x 2tan x

Something went wrong Wait a moment and try again Try again Please enable Javascript and refresh the page to continueI am unable to see why $$1 \tan^2 x= 1/\cos^2x$$ I have looked into the topic anad I am familiar with the reciprocal ratios of cosec, sec, and cot but cannot derive how this statement makes sense Any help on the topic would be very much appreciatedSimplify (1tan(x)^2)(1sin(x)^2) Rearrange terms Apply pythagorean identity Rewrite in terms of sines and cosines Simplify the expression Tap for more steps Apply the product rule to One to any power is one Apply pythagorean identity Cancel the common factor of

Lim X To 0 2 Tan X 2 Sin X X 2 Sin X Without L Hopital S Rule How Is My Procedure Wrong Mathematics Stack Exchange

Derivative Of Tan X Old Video Khan Academy

Sec ( x) − 2 = 0 sec ( x) 2 = 0 Add 2 2 to both sides of the equation sec ( x) = 2 sec ( x) = 2 Take the inverse secant of both sides of the equation to extract x x from inside the secant x = arcsec ( 2) x = arcsec ( 2) The exact value of arcsec ( 2) arcsec ( 2) is π 3 π 3 x = π 3 x = π 3RHs = (2 tan x cos 2 x 1 ) cos 2 x = 2 sin x cos x 1 = 1 sin 2 x If sin 2 x = t, then we have f t = 1 t, where t = sin 2 x where − 1 ≤ t ≤ 1 ∴ Domain is − 1, 1 Adding 1 throughout, 0 ≤ 1 t ≤ 2 or 0 ≤ f (t) ≤ 2 ∴ Range of f(t) is 0, 2Click here👆to get an answer to your question ️ If f(x) = cos^2x sec^2x , then

Tan2x ただの悪魔の画像

A 1 Tan X Tan X 1 Show That A Ta 1 Cos 2x Sin 2x Sin 2x Cos 2x Sarthaks Econnect Largest Online Education Community

  Use the fact that tanx = sinx cosx and sin2x = 2sinxcosx So 2 sinx cosx ⋅ 1 1 sinx cos2x = 2sinxcosx 2 sinx cosx ⋅ cos2x cos2x sin2x = 2sinxcosx 2 sinx cosx ⋅ cos2 x cos2x sin2x = 2sinxcosxTRIGONOMETRIC EQUATIONS An equation involving one or more trigonometrical ratios of unknown angle is called a trigonometric equation eg cos 2 x – 4 sin x = 1 It is to be noted that a trigonometrical identity is satisfied for every value of the unknown angle where as trigonometric equation is satisfied only for some values (finite or infinite) of unknown angleThe distance between 0 0 and 1 1 is 1 1 Divide 2 π 2 π by 1 1 The period of the sec ( x) sec ( x) function is 2 π 2 π so values will repeat every 2 π 2 π radians in both directions The final solution is all the values that make (tan(x)−1)(sec(x)− 1) = 0 ( tan ( x) 1) ( sec ( x) 1) = 0 true

Find All Solutions To The Equation Tan 2x 2tanx 1 0 Chegg Com

Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo

 Get an answer for 'verify (1 tan^2x)/(tan^2x) = csc^2x' and find homework help for other Math questions at eNotesSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreB = rsinθ r = √ (a²b²) θ = tan^1 (b/a) → make sure # and < are in right quadrant demoivres theorem if z = r (cosθ isinθ) then z⁹ = r⁹ (cos9θ isin9θ) if you want to find square root plug in 1/2 for n multiply/divide complex # z₁z₂ = r₁r₂ (cos (θ₁θ₂) isin (θ₁θ₂)) z₁/z₂ = r₁/r₂ (cos (θ₁

Qprove That Tan X 2 Tan 2x 4 Tan 4x 8 Cot 8x Cot X Mathematics Topperlearning Com Blpusg55

Q Tbn And9gcr2jamezvnschsup9wyxdzj0wc0knie4dqfphj6okqiboct8vn1 Usqp Cau

Trigonometry Solve for x tan (2x)= (2tan (x))/ (1tan (x)^2) tan (2x) = 2tan (x) 1 − tan2 (x) tan ( 2 x) = 2 tan ( x) 1 tan 2 ( x) Since x x is on the right side of the equation, switch the sides so it is on the left side of the equation 2tan(x) 1− tan2(x) = tan(2x) 2 tan ( x) 1 tan 2 ( x) = tan ( 2 x)Move 1 1 to the left side of the equation by subtracting it from both sides cos2(x) sin4(x) cos2(x) 1 = 0 cos 2 ( x) − sin 4 ( x) cos 2 ( x) − 1 = 0 Simplify with factoring out Tap for more steps Move 1 − 1 cos 2 ( x) 1 sin 4 ( x) cos 2 ( x) = 0 cos 2 ( x) − 1 − sin 4 ( x) cos 2 ( x) = 0 Use the identities $1 tan^2(x)=sec^2(x)$, $1cot^2(x)=cosec^2(x)$ and the definitions of the reciprocal trig functions This will give the answers up to an unknown sign, for which we need to known whether x is obtuse or acute

Tan2x ただの悪魔の画像

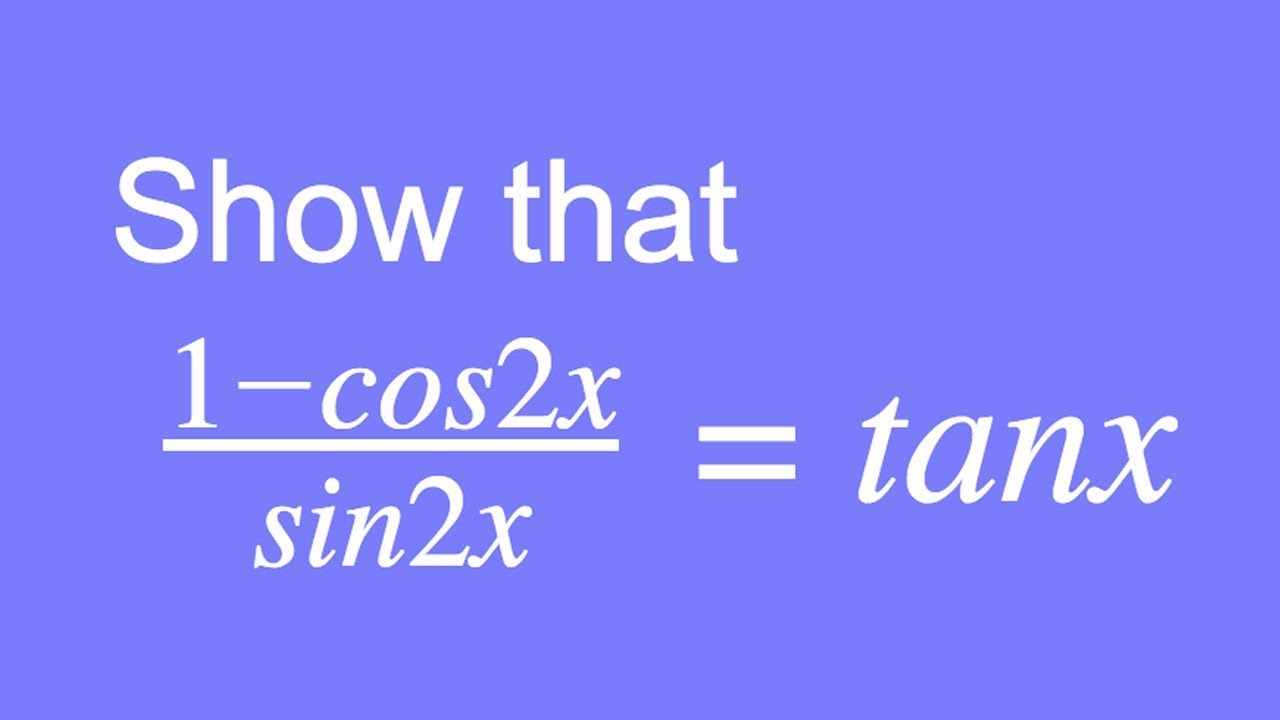
How To Show That 1 Cos2x Sin2x Tanx Youtube

Introduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula the opposite side is $$2tanx=2*2=4$$ the adjacent side is $$1tan^2x=12^2=14=3$$ (the negative sign just means it will not be in the first quad ) Using pythagoras the hypotenuse will be Misc 8 Find the value of sin 𝑥/2 , cos 𝑥/2 and tan 𝑥/2 in each of the following tan⁡𝑥 = – 4/3 , 𝑥 in quadrant II Given that x is in quadrant II So, 90° < x < 180° Dividing by 2 all sides (90°)/2 < 𝑥/2 < (180°)/2 45° < 𝑥/2 < 90° So, 𝑥/2 lies in Ist quadrant In 1st quadra

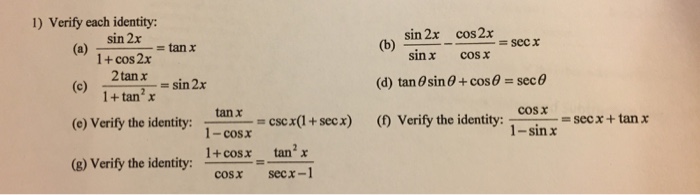
Verify Each Identity A Sin 2x 1 Cos 2x Tan X Chegg Com

Tan2x ただの悪魔の画像

Weekly Subscription $299 USD per week until cancelled Monthly Subscription $9 USD per month until cancelled Annual Subscription $3999 USD per year until cancelledSee the answer Show transcribed image text Expert Answer 100% (3 ratings) Previous question Next question Transcribed Image Text from this Question Prove the identity sec^2/2 tan x = csc 2xFirst, use the positive value of the ± ± to find the first solution tan ( x) = √ 3 3 tan ( x) = √ 3 3 Next, use the negative value of the ± ± to find the second solution tan ( x) = √ 3 3 tan ( x) = − √ 3 3 The complete solution is the result of both the positive and negative portions of the solution

F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2

Trig Identity Sec 4x Tan 4x 1 2tan 2x Youtube

(tan^2(x)1)/sec^2 = 12cos^2(x) Mulitiply by cos^2 (sin^2 cos^2)/1 = 1 2cos^2 Add cos^2 sin^2 = 1 cos^2 QED Answer by MathTherapy(9794) (Show Source) tan^4 (x) 1 or (tan^2(x)1)(tan^2x1) then i'm stuck! Ex 34, 8 Find the general solution of the equation sec2 2x = 1 – tan 2x sec2 2x = 1 – tan 2x 1 tan2 2x = 1 – tan2x tan2 2x tan2x = 1 – 1 tan2 2x tan2x = 0 tan 2x (tan2x 1) = 0 Hence We know that sec2 x = 1 tan2 x So, sec2 2x = 1 tan2 2x tan 2x = 0 taMathtan^2xcot^2x=2/math math\therefore tan^2x\dfrac{1}{tan^2x}2=22/math math\therefore \left(tanx\dfrac{1}{tanx}\right)^2=4/math math\therefore

3

bestpictjcry Tan 2x Tan 2x

Just observe that cos2xtan3x = tan3x sec2x = tan2x ⋅ tanx sec2x ⋅ 2sec2x 2sec2x = tan2x 2sec4x(2tanxsec2x) = tan2x (1 tan2x)2(tan2x) ′, thus the substitution t = tan2x gives ∫cos2xtan3xdx = ∫ t 2(1 t)2 dt Now the rest is clear Share edited Jun 3 '12 at 1656 answered Jun 3 '12 at 1646Question Prove The Identity Sec^2/2 Tan X = Csc 2x This problem has been solved!Click here👆to get an answer to your question ️ Prove that 2tan^1x = cos^1 ( 1 x^21 x^2 )

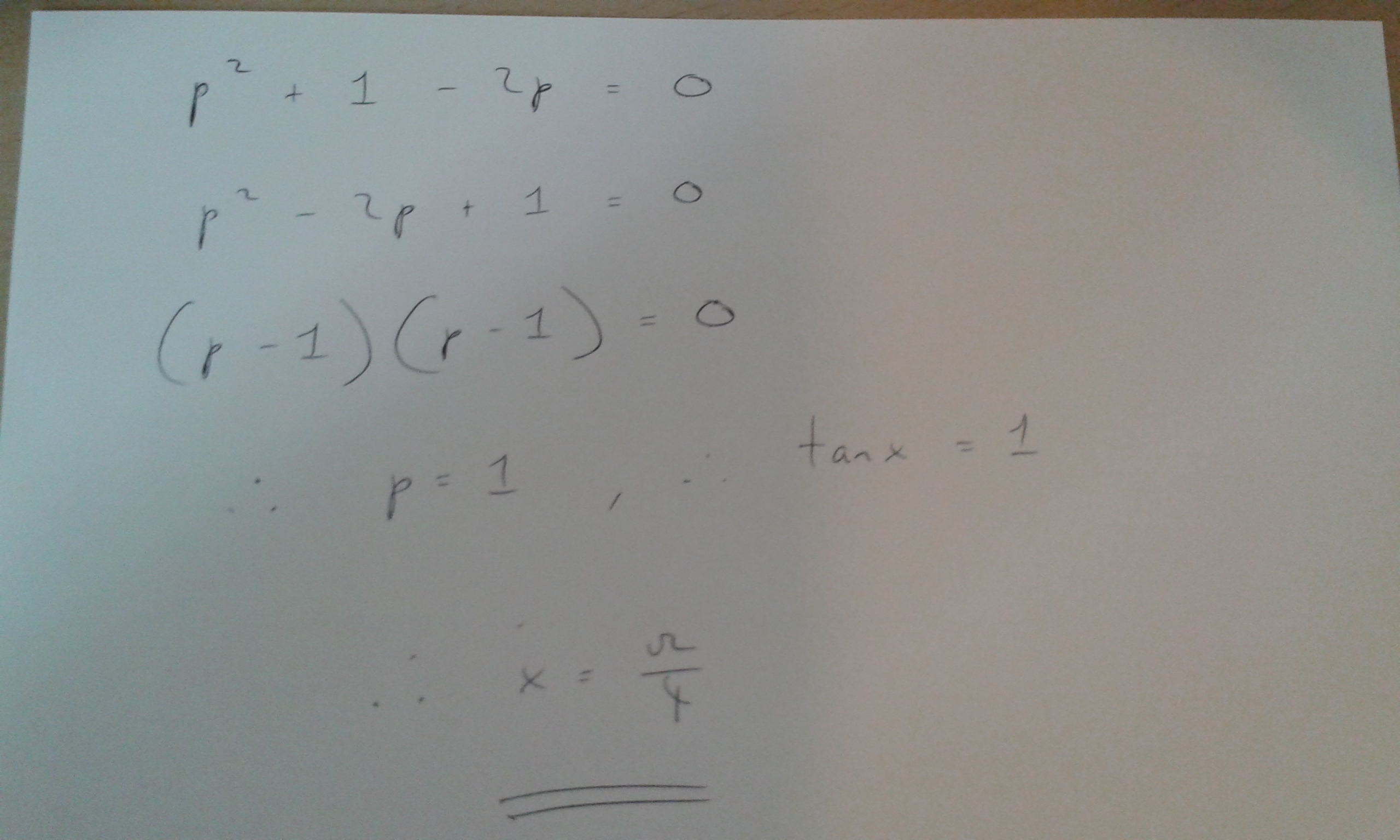
How Do You Solve Sec 2x 2tanx 0 Socratic

If F 2tanx 1 Tan 2x Cos2x 1 Sec 2x Tanx 2 Then F X

Sin(2x) = (2tan(x)) / (1tan^2(x)) *** Start with RHS 2tanx/(1tan^2x) 2tanx/(sec^2x) 2(sinx/cosx)/(1Solve for x sec(x)^22tan(x)=4 Replace the with based on the identity Reorder the polynomial Factor using the AC method Tap for more steps Consider the form Find a pair of integers whose product is and whose sum is In this case, whose product is and whose sum is f(2tanx/1tan 2 x)=(cos2x1) (sec 2 x2tanx)/2 then f(4) is equal to?

Integrate 1 Cos2x 1 Tanx 2 Maths Meritnation Com

Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco

 Explanation sec2x(1 −cos2x) = sec2x −sec2x × cos2x = sec2x − 1 cos2x ×cos2x = 1 tan2x − 1 cos2x × cos2x = 1 tan2x −1 = tan2x Answer link selected by subrita Best answer We have f (2tanx/ (1 tan2x)) = 1/2 (1 cos2x) (sec2x tanx) = 1/2x 2cos2x x (1 tan2x 2tanx) = cos2x x (1 tanx)2 = {cosx x (1 tanx)}2 = (cosx sinx)2 if sinx=7/5 and angle x is in quadrant 2 and cos y=12/13 and angle y is in quadrant 1 find sin (xy) asked in TRIGONOMETRY by harvy0496 Apprentice doubleangle

What Is The Integration Of 1 2tanx Tanx Secx 1 2 Dx Quora

Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2

 But is it equal to (2tanx/1tan^2x)^2 is what I'm asking I may have been unclearYou can put this solution on YOUR website!Prove as an identity;

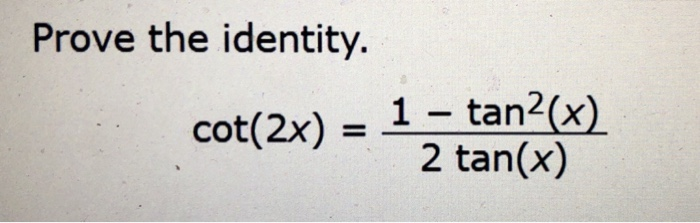
Prove The Identity Cot 2x 1 Tan2 X 2 Tan X Chegg Com

If F 2tanx 1 Tan 2x Cos2x 1 Sec 2x Tanx 2 Then F X

 Precalculus help I have two problems I am stuck on, if you could show me how to solve the problems it would be much appreciated 1) Find sin 2x, cos 2x, and tan 2x from the given information tan x = − 1/6, cos x > 0 sin 2x = cos 2x = tan 2x =Get an answer for 'Prove the following sin 2x = (tan x)(1 cos 2x)' and find homework help for other Math questions at eNotesFirst I join fractions (Easy) then I "express" tans in

Prove Sin2x 2tanx 1 Tan 2x Socratic

Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube

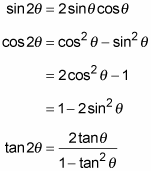
How Do You Prove That Cot2x Tan 2x 1 2tanx Socratic

Integration Calculus Notes

F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2

What Is The Formula Of Tan2x Quora

5 If F 2tan X 1 Tan 2 X Qquad Cos2x 1 Sec 2 X 2tan X

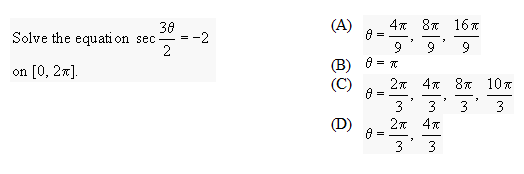
Find All Solutions To The Equation Tan 2x 2tanx 1 0 Chegg Com

Ex 7 2 25 Integrate 1 Cos 2 X 1 Tan X 2 Ex 7 2

F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2

Integral Of 1 Cos 2 X Sqrt 1 Tan X Calculus 1 Trig Integrals Youtube

Ovingtonclassroom Weebly Com Uploads 1 0 6 2 Chapter 4 Review Key Pdf

Limit X Tends P 4 Sec 2x 2 Tanx 1 Brainly In

1 Cos 4 X Sinº X Cos 2x 6 6 2 Sin X Cos X Homeworklib

Tan2x ただの悪魔の画像

Iit 1994 Prove That Sec2x Tan2x Tan Pi 4 X When X Lies Between 0 And Pi 4 Youtube

Tan2x ただの悪魔の画像

How To Find Least Value Of Cos 2 X Sec 2 X Quora

How To Take The Derivative Of Tan X Video Lesson Transcript Study Com

Tan2x ただの悪魔の画像

Cot X Cos 2 X Tan X Sin 2 X 2 Cot 2x Youtube

How Do You Solve Sec 2x 2tanx 0 Socratic

F4ntussz Z2tvm

Q45 Integral Of 1 Tan 2x Sec 2x Youtube

Tan2x ただの悪魔の画像

By Using Known Trig Identities Sin 2x 1 Cos 2x Chegg Com

Tan2x ただの悪魔の画像

If Tan X Cot X 2 Then What Is The Value Of Sin X Quora

Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2

What Is The Domain Of The Definition Of F X Sec 1 Cos 2x Quora

Integration Calculus Notes

Http Www Science Marshall Edu Karna Pdfdocfiles Examsingle 229exam2 Pdf

The Value Of Lim X Gt0 Xtan2x 2xtanx 1 Cos2x 2 Is Equal To Youtube

Http Www Science Marshall Edu Karna Pdfdocfiles Examsingle 229exam2 Pdf

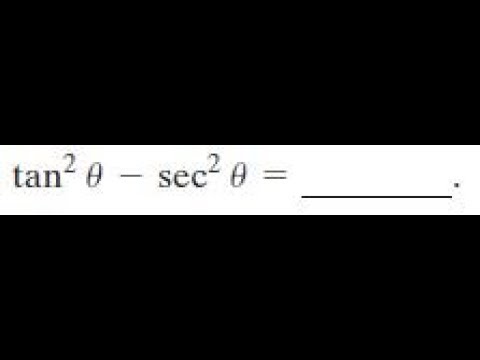
Tan 2x Sec 2x Youtube

Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x

If F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2 Then Domain And Range Of Y F X Are Given By

How To Prove That Lhs Rhs Sin2x 2tanx 1 Tan Square X Quora

Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo

Tan 2x 2tanx 5dy Dx 2 1 Tanx Sec 2x Differential Equations Brainly In

Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2

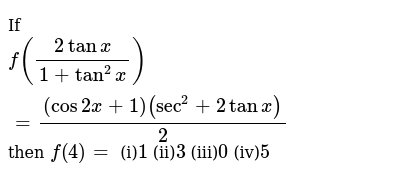
If F 2tanx 1 Tan 2 X Cos2x 1 Sec 2 2tanx 2 Then F 4 I 1 Ii 3 Iii 0 Iv 5

1

3

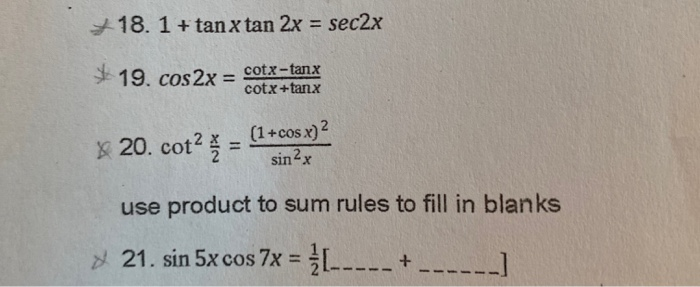
18 1 Tan X Tan 2x Sec2x 19 Cos2x Cotx Tank Chegg Com

How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Socratic

Chapter 9 Notes

F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2 Youtube

If F 2tanx 1 Tan 2x Cos2x 1 Sec 2x Tanx 2 Then F X

Find The Range Of F X Sqrt 4 Sqrt 1 Tan 2x

Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo

Evaluate Lim X P 4 Sec 2x 2tanx 1 Cos4x Sarthaks Econnect Largest Online Education Community

Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2

Integral Of 1 Cos 2x 1 Cos 2x Youtube

2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula

If F 2tanx 1 Tan 2x Cos2x 1 Sec 2x Tanx 2 Then F X

Limit Trigonometric Function 2 Sec 2x 1 Tan X Youtube

Proof For Tan 2x 2tanx 1 Tan X Trigonometry Youtube

Derivatives Of Tan X And Cot X Video Khan Academy

If F X 2tan X 1 Tan 2 X Then Value Of F Pi 4 Will Be

Prove The Identity Cot 2x 1 Tan 2 X 2 Tan X Chegg Com

If F Left Frac 2 Tan X 1 Tan 2 X Right Cos 2 X 1 Left Sec 2 X 2 Tan X Right 1 2 3 Quad 3 0 Quad 4 5

Juhfl atogwm

Calculus 9e Purcell Varberg Rigdon Solution

What Is The Formula Of Tan2x Quora

Tan2x ただの悪魔の画像

Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x

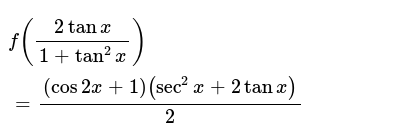
F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2

Powers Of Trigonometric Functions

What Is The Formula Of Tan2x Quora

Solve Int1 Cos 2x 1 Tanx 2dx

Old Version Show Sin 2x 2 Sin X Cos X 2tan X 1 Tan 2 X Youtube

1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube

Tanx 4 3 X In Quadrant Ii Find The Value Of Sinx 2 Cosx 2 Tanx 2

How Would You Evaluate Lim X Tending To P 4 1 Tan X Cos 2x Using L Hospital S Rule Quora

Calculate Sin2x Cos2x And Tan2x For Given Tanx In Quadrant 2 Youtube

Integral Of Tan X Sec 2 X Two Results Off By A Constant Youtube

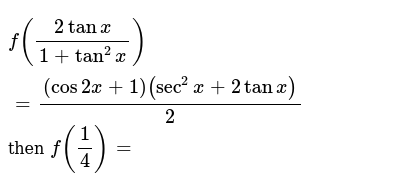
F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2 Then F 1

1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube

Trigonometry Solutions Manual